Home 3$

View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then

By A Mystery Man Writer

Last updated 17 Jun 2024

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Free Online Scientific Notation Calculator. Solve advanced problems in Physics, Mathematics and Engineering. Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History.

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Consider the recursive sequence x1 = 2, xn+1 = 1 +

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved We are looking at sequences x1,x2,…,x2n such that for

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

SOLVED: Subsequences of convergent sequences also converge to the same limit. As we now show: 3.4.2 Theorem: If a sequence X = (xn) of real numbers converges to a real number x

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

math-solutions/Hartshorne/Hartshorne Solutions.tex at master · awasthi/math-solutions · GitHub

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Consider the series. in Σ n=1 (n2 + 1)24 7x Let f(x)

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Let a sequence X0, X1, X2, be defined in the

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Let a sequence X0, X1, X2, be defined in the

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

SOLVED: The sequence (xn) is defined by the recursion relation: x1 = 2, xn+1 = xn^2 + 1, for n = 1,2,3. Prove that: For all n, xn âˆˆ [2,4]. xn^2 =

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Are the following sets countable? The set of finite

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

SOLVED: 3.2.10 Theorem: Let X = (xn) be a sequence of real numbers that converges to x, and suppose that xn â‰¥ 0. Then the sequence âˆšxn of positive square roots converges

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Exercise 2.3.11 (Cesaro Means). (a) Show that if (xn)

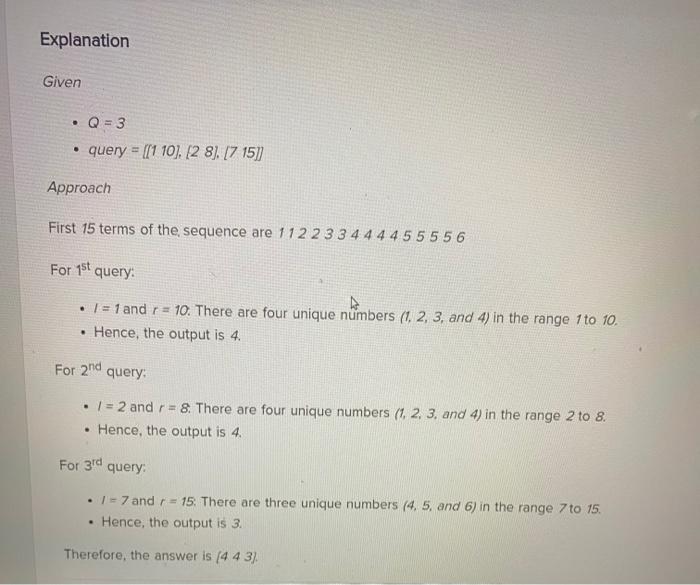
$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

Solved Unique numbers Consider a sequence of integers as 1

$View question - The sequence $x_1$, $x_2$, $x_3$, . . ., has the property that $x_n = x_{n - 1} + x_{n - 2}$ for all $n \ge 3$. If $x_{11} - x_1 = 99$, then$

1 Chapter Facts about Functions. 2 Section 2.1 Functions: Definitions and Examples A function ƒ from A to B associates each element of A with exactly. - ppt download

Recommended for you